从二维绘图到数值优化——初探 golang 科学计算包 gonum

. Golang

目录

gonum 简介

image

gonum 是一个用 golang 写的数学工具包，包括矩阵计算、数理统计、数值优化等等。GitHub 上，目前该项目拥有 3.4k 的 stars，超过 5000 次提交，并且仍保持着活跃更新。

gonum 项目所属的组织也叫 Gonum（此处故意大写，方便区分），这个组织下还有一个独立的包 plot，用于数据可视化，而脱离可视化去使用 gonum 是很枯燥的，所以若无特别说名，本文说的“gonum 包”，实际上是指 Gonum 组织下 gonum、plot 等包的集合，而不是单指 gonum 这一个包。

Gonum 有一个官网：www.gonum.org，但很遗憾目前网站上并没有多少实质性的内容，也没相关的教程或文档，从网上找到的一些资料不仅不多，而且老旧的很，与新版的代码不相符。

所以本文是我为了解决工作中的一些问题，想借助 gonum 做一些数值分析时，在没有权威文档的情况下，靠四处搜罗、阅读代码、主观臆测，总结而来的一个 gonum 的简单教程。由于我的初衷带有强烈的目的性，所以本文的目的性也很强，主要是在解决数值优化（Numerical Optimization）这一类型的问题，所以并不能覆盖 gonum 所有的功能。

但本文仍然可以帮助读者初识一下 gonum，并可能带来一些帮助或启发。由于我水平有限，且一直弱于数学，若有纰漏，还望指正。

下面正式开始。

画些点线

首先我们利用 gonum 画一些简单的点线，为后面打下基础，有了数据可视化工具，乐趣会多上很多。

首先要安装 gonum，这并不麻烦，运行一行命令即可：

go get -u gonum.org/v1/gonum/...

不过如果你更乐意用 dep 或 module 来进行包管理，那么我相信你自然会用对应的命令来安装这个包，这里就不赘述了。

先画一个一次函数的图像，也就是一条线：

package main

import (
	"gonum.org/v1/plot"
	"gonum.org/v1/plot/plotter"
	"gonum.org/v1/plot/plotutil"
	"gonum.org/v1/plot/vg"
)

func main() {
	var a, b float64 = 0.7, 3
	points := plotter.XYs{}
	for i := 0; i <= 10; i++ {
		points = append(points, plotter.XY{
			X: float64(i),
			Y: a*float64(i) + b,
		})
	}

	plt, err := plot.New()
	if err != nil {
		panic(err)
	}
	plt.Y.Min, plt.X.Min, plt.Y.Max, plt.X.Max = 0, 0, 10, 10

	if err := plotutil.AddLines(plt,
		"line1", points,
	); err != nil {
		panic(err)
	}

	if err := plt.Save(5*vg.Inch, 5*vg.Inch, "01-draw-line.png"); err != nil {
		panic(err)
	}
}
// 完整代码： https://github.com/wolfogre/gonum-example/blob/master/01-draw-line/main.go

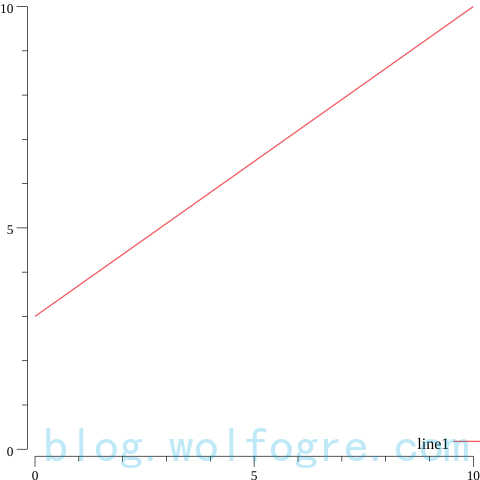
image

上面的代码绘制了 y = 0.7x + 3 在 x = [0, 10] 上的图像，从中我们可以看到这些事情：

  1. 类型 plotter.XYs 可以方便描述一组二维向量，即一个 plotter.XY 数组，顾名思义，plotter.XY 拥有 X 和 Y 两个字段；
  2. plot.New() 可以获得一个二维坐标系，我们可以通过一些可选操作来设置坐标系各个轴的最大值和最小值，帮助图像展示得更合理；
  3. plotutil 是个辅助工具，可以帮助我们将 plotter.XYs 转换为 Line 并绘制到坐标系上，当然我们也可以不借助它，自己构造 plotter.Line 对象并 Add 到坐标系上；
  4. 由于 golang 尚没有成熟的 GUI 组件，或者说 gonum 目前没有集成任何 GUI 组件，所以如果我们想看到绘图结果，需要将 plot.Plot 对象保存成图像文件查看。

这张图有点单调，只有一条线，且线上也没有标注数据点，所以我们可以稍微修改下代码：

// ...

func main() {
	var a, b float64 = 0.7, 3
	points1 := plotter.XYs{}
	points2 := plotter.XYs{}

	for i := 0; i <= 10; i++ {
		points1 = append(points1, plotter.XY{
			X: float64(i),
			Y: a*float64(i) + b,
		})
		points2 = append(points2, plotter.XY{
			X: float64(i),
			Y: a*float64(i) + b + (2*rand.Float64() - 1),
		})
	}

	// ...

	if err := plotutil.AddLinePoints(plt,
		"line1", points1,
		"line2", points2,
	); err != nil {
		panic(err)
	}

	// ...
}
// 完整代码：https://github.com/wolfogre/gonum-example/blob/master/02-draw-linepoint/main.go

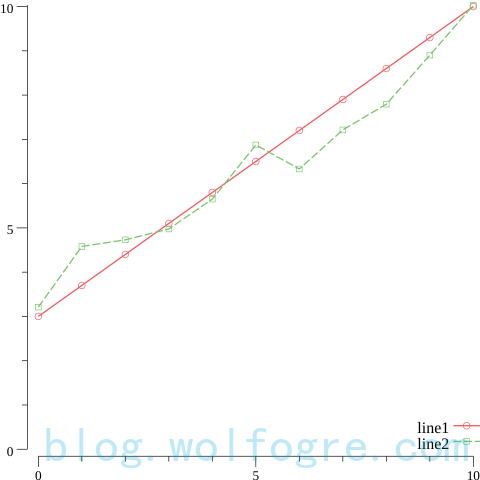
image

如你所见，我们又添加了一条折线，它是 y = 0.7x + 3 + random(-1, 1)。除此之外，我们在线上标注了数据点，可以更准确的看到数据的位置。

你是不是想到了，我们可以把 line1 当成目标函数，把 line2 当成观测值，那么通过 line2 去求 line1，就是个线性回归问题了。

那就试试吧，我们可以写一个最小二乘法的算法，求一个拟合值，这并不困难。

// ...

func main() {
	// ...

	fa, fb := LeastSquares(points2)
	points3 := plotter.XYs{}
	for i := 0; i <= 10; i++ {
		points3 = append(points3, plotter.XY{
			X: float64(i),
			Y: fa*float64(i) + fb,
		})
	}

	// ...

	if err := plotutil.AddLinePoints(plt,
		"line1", points1,
		"line2", points2,
		"line3", points3,
	); err != nil {
		panic(err)
	}

	// ...
}

func LeastSquares(points plotter.XYs) (a, b float64) {
	var xSum, ySum float64
	for _, point := range points {
		xSum += point.X
		ySum += point.Y
	}
	xAvg, yAvg := xSum/float64(points.Len()), ySum/float64(points.Len())

	var xySum, xxSum float64
	for _, point := range points {
		xySum += (point.X - xAvg) * (point.Y - yAvg)
		xxSum += (point.X - xAvg) * (point.X - xAvg)
	}

	a = xySum / xxSum
	b = yAvg - a*xAvg
	return
}
// 完整代码：https://github.com/wolfogre/gonum-example/blob/master/03-least-squares/main.go

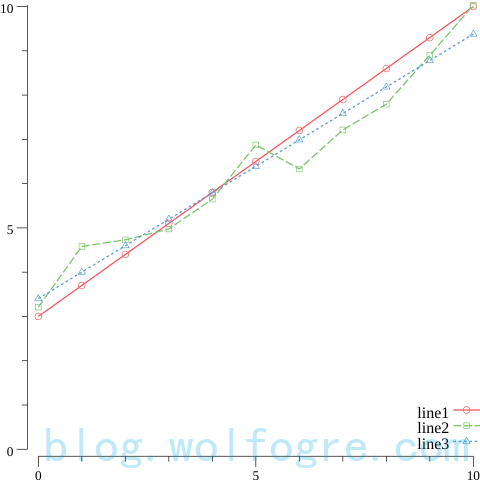
image

其中 line3 就是利用最小二乘法拟合的结果。

你可能会犯嘀咕了，这里还要手写最小二乘法的代码，而既然 gonum 是用来科学计算的，就没有现成的函数拿来用吗。别急，我这里只是抛出一个引子，好戏还在后面。

画热图

除了画线，画些单纯的点也是可以的。plotter.XYs 只是平面上的点集合的数据表示，转换成对应的可绘制对象则是 plotter.Scatter。而因为 plotutil.AddScatters 并不方便控制点的形状，所以这次我们不借助 plotutil，直接构造一个 scatter 并添加到 plot 上：

// ...

func main() {
	points := plotter.XYs{}
	for i := 0; i < 10; i++ {
		points = append(points, plotter.XY{
			X: 100 * rand.Float64(),
			Y: 100 * rand.Float64(),
		})
	}

	scatter, err := plotter.NewScatter(points)
	if err != nil {
		panic(err)
	}
	scatter.Shape = draw.CircleGlyph{}

	plt, err := plot.New()
	if err != nil {
		panic(err)
	}
	plt.Y.Min, plt.X.Min, plt.Y.Max, plt.X.Max = 0, 0, 100, 100

	plt.Add(scatter)

	// ...
}
// 完整代码：https://github.com/wolfogre/gonum-example/blob/master/04-draw-dot/main.go

image

如你所见，我们随机生成了 10 个点，并把它画到了坐标系上。

下面我们来画热图，为了方便画这个图，我们先得定义一下此处的“热度”概念，这里约定：图上任意一处的“热度”，是该处距离所有点距离之和的相反数，也就是说，该处距离所有黑点的距离之和越小，则越“热”。

有了这个粗糙的概念，我们就可以画热图了：

// ...

func main() {
	// ...

	heatmap := plotter.NewHeatMap(Heat(points), moreland.SmoothBlueRed().Palette(100))

	// ...

	plt.Add(heatmap, scatter)
	
	// ...
}

type Heat plotter.XYs

func (h Heat) Dims() (c, r int) { return 100, 100 }
func (h Heat) X(c int) float64  { return float64(c) }
func (h Heat) Y(r int) float64  { return float64(r) }
func (h Heat) Z(c, r int) float64 {
	var sum float64
	for _, p := range h {
		sum += math.Sqrt(math.Pow(p.X-h.X(c), 2) + math.Pow(p.Y-h.Y(r), 2))
	}
	return -sum
}
// 完整代码：https://github.com/wolfogre/gonum-example/blob/master/05-draw-headmap/main.go

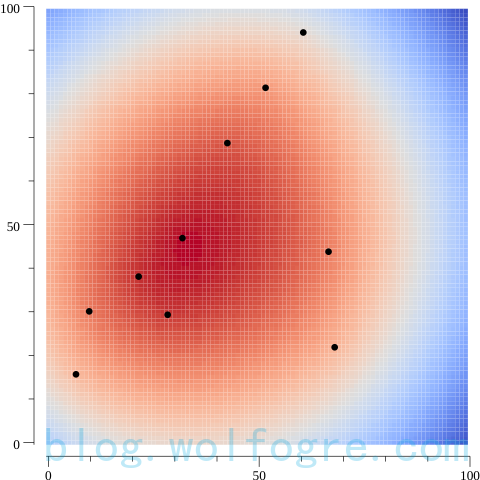
image

你可能意识到了，热图其实就是用颜色大致地表示平面坐标上各个点 Z 轴的值，所以有了热图，我们有了一种在二维平面上绘制三维向量的方法，这是件很有意义的事情。

数值优化问题

再继续写代码之前，我们需要补充一些背景知识，解释一下什么是“数值优化”。

数值优化（Numerical Optimization）是应用数学的一个分支，主要研究在特定情况下最大化或最小化某一特定函数或变量。

如果你觉得这样的定义不好理解，那可以换个思路，回头看上面那张热力图，假设你是一只蚂蚁，你要在图中找一个最温暖的地方呆着，那么，有没有什么算法能找到这个点呢？这是一个很形象的数值优化问题示例，这里的特定函数 f(x, y) 是“点 (x, y) 距离指定 10 个点的距离的和”，而我们要找到一个点 (x, y) 使得 f(x, y) 的值最小。为了后面描述方便，我们管这个函数叫代价函数。很显然，代价函数的参数是一个向量，这意味着需要解决的问题不仅可以面向二维，也可以面向一维（f(x)）、三维（f(x, y, z)）以及高维（f(x, y, z...)）。

但这个蚂蚁寻热问题其实并不具有代表性，实际上，你想一想就会发现，最优解就是拿 10 个点 X 的平均值做 x，10 个点 Y 的平均值做 y，(x, y) 即为最优解。既然如此，那我们还搞什么数值优化呢，不是可以直接计算得出结果吗？

是的，有些情况下，当代价函数比较简单或者满足特定条件的时候，是可以直接求出最优解的，这样的解叫解析解。但有的时候实际问题可能不会这么简单，代价函数可能非常复杂，并不具备计算解析解的可能，这时候只能通过数值分析的方法求解近似值，即数值解。

还记得前文那个线性回归的例子吗，其实它也是一个这样的问题，代价函数 f(a, b) 是 y = ax + b 和观测到的数据的误差，而我们需要找出一个 (a, b) 使得误差最小。

而衡量误差的方法有很多种，最小二乘法是将误差设为“观测值与拟合值之间的差的平方和”，你应该会疑惑，为啥非要是平方和，不可以是绝对值总和或着其他形式吗，答案就是：因为取平方和刚好可以让代价函数可以求出解析解，而最小二乘法其实就是求这个代价函数的解析解的方法。如果代价函数稍稍变动一下，比如改为“观测值与拟合值之间的差距的绝对值总和”，那最小二乘法就瞬间失效。

这时候，数值优化就闪亮登场了。

描述问题

如何将数值优化问题抽象成 golang 代码，gonum 在这一点上做的非常精巧。用于描述数值优化问题的结构是 gonum.org/v1/gonum/optimize.Problem，它的定义如下：

type Problem struct {
	Func func(x []float64) float64
	Grad func(grad, x []float64)
	Hess func(hess *mat.SymDense, x []float64)
	Status func() (Status, error)
}

四个字段都是函数类型，乍一看可能很麻烦，但结合前文的背景知识并不难理解。

第一个是 Func，它就是我们上文说的代价函数，它的输入是一个向量，返回的是该向量对应的“代价值”。所以你会发现，其实只要传入了 Func，就已经完整的描述了问题，而事实也确实如此，其他三个字段确实是可以为空的。那为什么还需要其他字段呢，概括地说就是：“其他字段是为了帮助更好的解决问题”。

Grad 存放的是代价函数对应的导数，严格来说，这里叫“梯度”才更准确，这里不细究，可以用导数来理解。可想而知，梯度的方向指示了极值的所在的相对方向，有了函数对应的梯度，在求解的过程中可以更快地收敛到极值。

Hess 存放的是代价函数的黑塞矩阵，关于黑塞矩阵是什么可以看维基百科的解释，坦白说，我看了半天也没看懂，但简单理解就是，它也是为了帮助某些数值优化算法，一般指牛顿法，更好更快地找到极值。

最后的 Status 则是为了方便我们控制优化计算过程，绝大多数情况下我们不用特意设置它，直接忽略好了。

我们仍然以上文的蚂蚁寻热问题为例子，构造一个 Problem：

// ...

func main() {
	// ...

	Func := func(x []float64) float64 {
		if len(x) != 2 {
			panic("illegal x")
		}
		var sum float64
		for _, point := range points {
			sum += math.Sqrt(math.Pow(point.X-x[0], 2) + math.Pow(point.Y-x[1], 2))
		}
		return sum
	}

	problem := optimize.Problem{
		Func:   Func,
		Grad:   nil,
		Hess:   nil,
		Status: nil,
	}

	_ = problem
}
// 完整代码：https://github.com/wolfogre/gonum-example/blob/master/06-problem/main.go

可以看到，我们只填充了 optimize.Problem 的 Func 字段，其他字段均留空，这已经完整地描述了问题了。但需要注意的是，“代价函数”是个贬义词，意味着越小越好，所以这里的代价函数的定义是“该处距离所有点距离之和”，注意没有取相反数，这与上文的“热度”定义有细微区别，但本质是一样的。

但因为缺乏梯度函数和黑塞矩阵，而有些数据优化算法又是需要这两个参数（或其中之一）的，所以不是所有的数据优化算法都适用这里定义的 Problem，但这并不影响这个 Problem 是个可解决的问题。

下山单纯形法

下山单纯形法，也称 Nelder–Mead 方法，是我们前文提到的数值优化算法之一，它的特点是可应用于非线性优化问题，换句话说，它不要求代价函数可导，所以也就不要求我们提供梯度函数或黑塞矩阵了。

用它来处理上一节那个既没有 Grad 也没有 Hess 的 Problem 自然再合适不过。而这次不需要我们自己写算法实现了， gonum 自带了这个算法。

// ...

func main() {
	// ...

	Func := func(x []float64) float64 {
		if len(x) != 2 {
			panic("illegal x")
		}
		var sum float64
		for _, point := range points {
			sum += math.Sqrt(math.Pow(point.X-x[0], 2) + math.Pow(point.Y-x[1], 2))
		}
		return sum
	}

	problem := optimize.Problem{
		Func: Func,
	}

	result, err := optimize.Minimize(problem, []float64{1, 1}, &optimize.Settings{}, &optimize.NelderMead{})
	if err != nil {
		panic(err)
	}

	aim, err := plotter.NewScatter(plotter.XYs{{
		X: result.X[0],
		Y: result.X[1],
	}})
	if err != nil {
		panic(err)
	}
	aim.Shape = draw.CircleGlyph{}
	aim.Color = color.White

	// ...

	plt.Add(heatmap, scatter, aim)

	// ...
}

// ...
// 完整代码：https://github.com/wolfogre/gonum-example/blob/master/07-nelder-mead/main.go

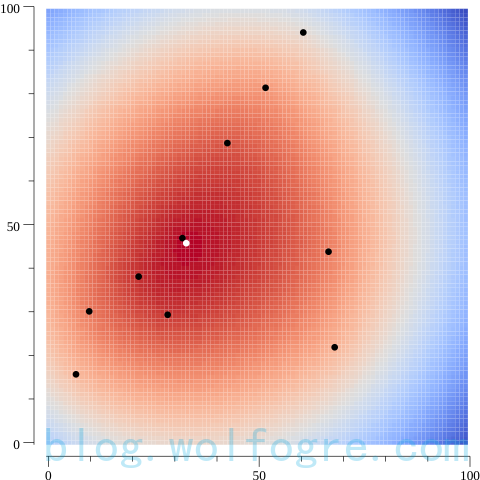
image

图中白色的点，就是得出的最优点了，目测的话，它的确是图中最“热”的点。

解决这个问题的关键函数是：

func optimize.Minimize(p Problem, initX []float64, settings *Settings, method Method) (*Result, error)

顾名思义，Minimize 就是要求出“最小值”，参数分别是：

  • p Problem：求解的数值优化问题，这里就是“蚂蚁寻热”的问题；
  • initX []float64：初始坐标，即从什么位置开始搜索最优解，这里是随便给的 (1, 1)；
  • settings *Settings：一些求解过程中的可选配置，这里给的是空配置，即用默认配置；
  • method Method：用什么数值优化算法来求解问题，这里给的是 optimize.NelderMead，即 gonum 自带的下山单纯形法实现。

返回值 Result 中最重要的字段就是 Result.X 了，它是一个向量，和初始坐标 initX 的维数是一样的，是最优解的坐标。

虽然我们成功得到了答案，不过遗憾的是，我们只是用白色的点来展示了最优求解的结果，却没有展示求解的过程，这实在差了那么点意思，也枉费了我们前面花那么大力气学习画点画线不是？

图示求解过程

为了记录求解的中间步骤，我们需要在参数 settings *Settings 中设置一个记录器，即 Recorder，来记录每次尝试求解的坐标。得到了这一系列坐标，再想图形化展示出来就容易了。

// ...

func main() {
	// ...

	recorder := &Recorder{}

	result, err := optimize.Minimize(problem, []float64{1, 1}, &optimize.Settings{
		Recorder: recorder,
	}, &optimize.NelderMead{})
	if err != nil {
		panic(err)
	}

	pathLines, pathPoints, err := plotter.NewLinePoints(recorder.XYs)
	if err != nil {
		panic(err)
	}

	// ...

	plt.Add(heatmap, scatter, pathPoints, pathLines, aim)

	// ...
}

// ...

type Recorder struct {
	XYs plotter.XYs
}

func (r *Recorder) Init() error {
	return nil
}

func (r *Recorder) Record(location *optimize.Location, op optimize.Operation, _ *optimize.Stats) error {
	if op != optimize.MajorIteration && op != optimize.InitIteration && op != optimize.PostIteration {
		return nil
	}
	r.XYs = append(r.XYs, plotter.XY{
		X: location.X[0],
		Y: location.X[1],
	})
	return nil
}
// 完整代码：https://github.com/wolfogre/gonum-example/blob/master/08-nelder-mead-with-recorder/main.go

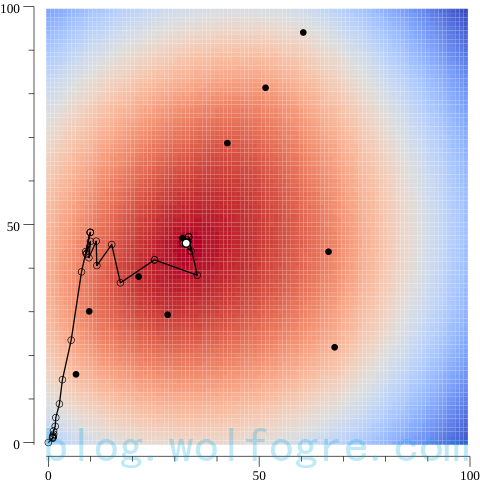
image

图中的折线，即是求解过程中每一步的尝试坐标，经过若干次的尝试，最终收敛到了最优解上。不过你应该也发现了，图中的求解路径明显不是最高效的，有几步甚至是在原地踏步，这其实也容易理解，因为缺乏梯度函数的指示，下山单纯形法的每次尝试。并不一定是沿着最佳方向作出的。

那还有没有其他算法可以拿来用呢？

使用其他算法

当前版本（v0.6.0）的 gonum 提供了 9 种数值优化算法的实现，分别是：

这里我做了一下简单的比较，主要针对适用性而言，并不是性能上的比较。

方法名称 代价函数 梯度函数 黑塞矩阵 适用生产
BFGS 需要 需要 不需要 是
CG 需要 需要 不需要 是
CmaEsChol 需要 不需要 不需要 是
GradientDescent 需要 需要 不需要 是
GuessAndCheck 需要 不需要 不需要 否
LBFGS 需要 需要 不需要 是
ListSearch 需要 不需要 不需要 否
NelderMead 需要 不需要 不需要 是
Newton 需要 需要 需要 是

可以看到，只要提供了代价函数和梯度函数，即使没有黑塞矩阵我们也可以使用绝大多数算法了。拿纸拿笔推导出导数固然是求梯度函数的最佳方式，但上文的蚂蚁寻热问题，并不容易求导，但我们知道，可以取 x1 点所在的极小区间内的 f(x) 的变化率来替代 x1 点的导数，这样就能方便的得出所需的梯度函数了。

而对于黑塞矩阵的计算，非常抱歉，我实在无能为力了。虽然我确实很想展示一下上面列举的所有的算法的使用，但不得不单独排除掉牛顿法，确有遗憾，还望理解。

// ...

func main() {
	// ...

	Func := func(x []float64) float64 {
		if len(x) != 2 {
			panic("illegal x")
		}
		var sum float64
		for _, point := range points {
			sum += math.Sqrt(math.Pow(point.X-x[0], 2) + math.Pow(point.Y-x[1], 2))
		}
		return sum
	}
	Grad := func(grad, x []float64) {
		if len(grad) != len(x) {
			panic("illegal grad or x")
		}
		delta := 1e-9
		for i, v := range x {
			x[i] = v - delta
			f1 := Func(x)
			x[i] = v + delta
			f2 := Func(x)
			x[i] = v
			grad[i] = (f2 - f1) / (2 * delta)
		}
	}

	problem := optimize.Problem{
		Func: Func,
		Grad: Grad,
	}

	methods := []struct {
		Name   string
		Method optimize.Method
	}{
		{"BFGS", &optimize.BFGS{}},
		{"CG", &optimize.CG{}},
		{"CmaEsChol", &optimize.CmaEsChol{}},
		{"GradientDescent", &optimize.GradientDescent{}},
		{"GuessAndCheck", &optimize.GuessAndCheck{
			Rander: distmv.NewUniform([]r1.Interval{{0, 100}, {0, 100}}, xrand.NewSource(0)),
		}},
		{"LBFGS", &optimize.LBFGS{}},
		{"ListSearch", &optimize.ListSearch{
			Locs: mat.NewDense(6, 2, []float64{
				0, 10,
				20, 30,
				40, 50,
				60, 70,
				80, 90,
				90, 100,
			}),
		}},
		{"NelderMead", &optimize.NelderMead{}},
		//{"Newton", &optimize.Newton{}}, // what a pity
	}

	for _, method := range methods {
		recorder := &Recorder{}

		result, err := optimize.Minimize(problem, []float64{1, 1}, &optimize.Settings{
			Recorder: recorder,
		}, method.Method)
		if err != nil {
			panic(err)
		}

		// ...
	}
}

// ...
// 完整代码：https://github.com/wolfogre/gonum-example/blob/master/09-other-methods/main.go

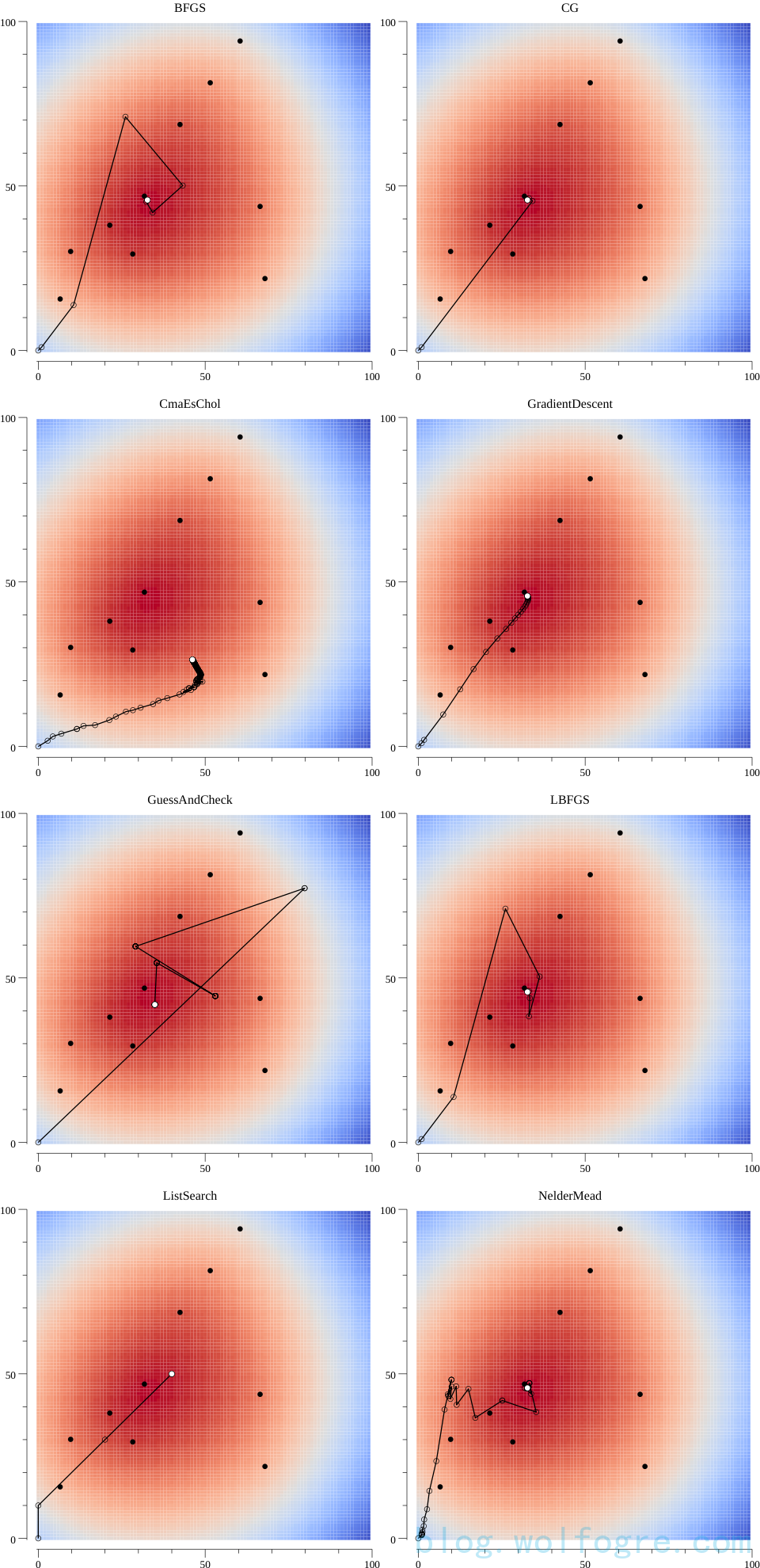
image

用数值优化来回归

花了这么大篇幅，相信你对 gonum 以及数值优化问题已经不再陌生。但上文的蚂蚁寻热问题固然直观，但并不是一个有代表性的真实问题。

还记得为什么我们会引出数值优化这一个方法吗？文章一开始，我们手写了最小二乘法来进行线性回归，但最小二乘法只适用于将偏差定义为“观测值与拟合值之间的差的平方和”，对于其它情况则无能为力。

现在有了数值优化这一手段，我们可以回过头来，高屋建瓴地再去看这个问题。

不管如何定义拟合的偏差，它一定可以抽象成一个代价函数，无论代价函数定义地如何复杂，只要它是可计算的，且存在最优解，那便可以用数值优化进行无差别打击。这种上帝视角的感觉实在是太好了。

我们这里修改一下拟合的偏差定义，改为“观测值与拟合值之间的差的绝对值的和”，而你完全可以自由发挥，根据你的实际需要来定义偏差，不必担心如何求解。

// ...

func main() {
	var a, b float64 = 0.7, 3
	points1 := plotter.XYs{}
	points2 := plotter.XYs{}

	for i := 0; i <= 10; i++ {
		points1 = append(points1, plotter.XY{
			X: float64(i),
			Y: a*float64(i) + b,
		})
		points2 = append(points2, plotter.XY{
			X: float64(i),
			Y: a*float64(i) + b + (2*rand.Float64() - 1),
		})
	}

	result, err := optimize.Minimize(optimize.Problem{
		Func: func(x []float64) float64 {
			if len(x) != 2 {
				panic("illegal x")
			}
			a := x[0]
			b := x[1]
			var sum float64
			for _, point := range points2 {
				y := a*point.X + b
				sum += math.Abs(y - point.Y)
			}
			return sum
		},
	}, []float64{1, 1}, &optimize.Settings{}, &optimize.NelderMead{})
	if err != nil {
		panic(err)
	}

	fa, fb := result.X[0], result.X[1]
	points3 := plotter.XYs{}
	for i := 0; i <= 10; i++ {
		points3 = append(points3, plotter.XY{
			X: float64(i),
			Y: fa*float64(i) + fb,
		})
	}

	// ...
}
// 完整代码：https://github.com/wolfogre/gonum-example/blob/master/10-optimize-fit/main.go

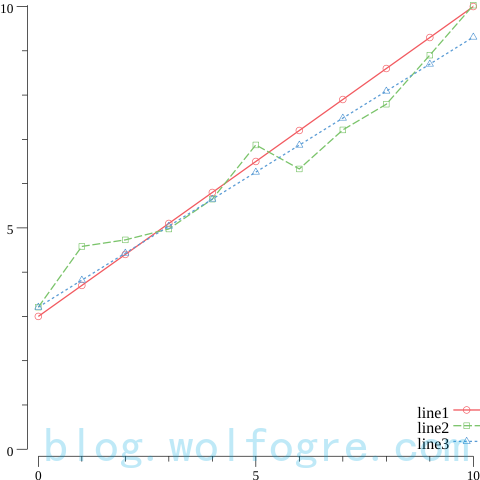
image

图中 line3 便是使用数值优化得出的线性拟合结果。

最后

何止于此！

你一定会感叹，用数值优化来解最简单的线性回归，实在是没有完全展现它的威力。而 gonum 所能做的，也绝不仅是数值优化，它也涵盖了矩阵计算、线性代数、概率统计、差分运算、网络拓扑等数学领域的常用模型和工具。

诚然，无论是成熟度还是丰富度，gonum 于 golang，尚不足以媲美 numpy 于 python，但它的诞生并不是为了比的，它让 golang 开发者不必切换语言，便可使用现成的数学工具来解决一些实际问题，这才是最大的价值所在。

参考

评论加载中……

若长时间无法加载，请刷新页面重试，或直接访问。